MRI Conductivity

Notice:

An applicant for an academic licence must provide the full name of their relevant organisation otherwise the application will be rejected.

Quantitative Conductivity Mapping (QCM) is a non-invasive technique that calculates the high-frequency tissue electrical conductivity (σ) from the phase (φ0) of the MRI signal1. QCM has a range of potential clinical applications including measuring sodium levels2, and distinguishing between different types of brain glioma3.

a) Laplacian-based methods

Most QCM methods are based on the following differential equation1, valid in regions with slowly varying σ:

σ = (μ0ω)-1⋅∇2φ0 [1]

where μ0 is the vacuum permeability, ω is the proton Larmor frequency, and ∇2 is the Laplacian operator. Applying a finite-difference approximation of ∇2 severely amplifies the noise4 (Figure 1a), which is why most current methods fit a 3D quadratic function within a kernel (Figure 1b) around each voxel and calculate the Laplacian of these fitted functions5,6. This 3D quadratic fit is usually either i) weighted by the magnitude values within the kernel5 (Figure 1c) or ii) restricted to voxels from the same tissue type7 (Figure 1d) to avoid artifacts at the conductivity boundaries where Eq. 1 is not applicable.

While these are the most commonly used methods for QCM, there is a lack of readily available implementations that could be used as a standard. Here, we have implemented a MATLAB function that performs QCM by quadratic fitting within an ellipsoidal kernel of user-defined dimensions and with options for i) magnitude- or ii) segmentation-based edge preservation. Moreover, i) and ii) can be used in combination (Figure 1e), which is a new approach that shows promise for outperforming all the other techniques (Figure 1).

b) Surface-integral-based methods

Eq. 1 can also be formulated as a surface integral8 that has previously been suggested to be more noise-robust than the differential form9:

σ = (μ0ωV)-1⋅∫S ∇φ0 [2]

where S is a closed surface of some kernel with volume V. To solve this equation, only the first derivatives of φ0 need to be calculated which induces less noise amplification then estimating the Laplacian. ∇φ0 can be calculated using the 3D quadratic fitting approach described above. Since Eq. 2 is also not valid at the conductivity boundaries, i) magnitude-, and/or ii) segmentation-based restrictions can be applied to both kernels (one for calculating ∇ and another one for calculating the surface integral).

Though we have recently shown that the integral-based methods are more accurate than the differential-based approaches (Figure 1), very few studies have previously applied these (using small kernels only without i) or ii)) possibly because the surface integral is tricky to implement. Here, we have implemented a MATLAB function that performs QCM by solving Eq. 2 with options for i), ii), or i) and ii) combined. These methods are all entirely new.

By disseminating this software, we hope to accelerate QCM research and its translation into a wide range of clinical applications.

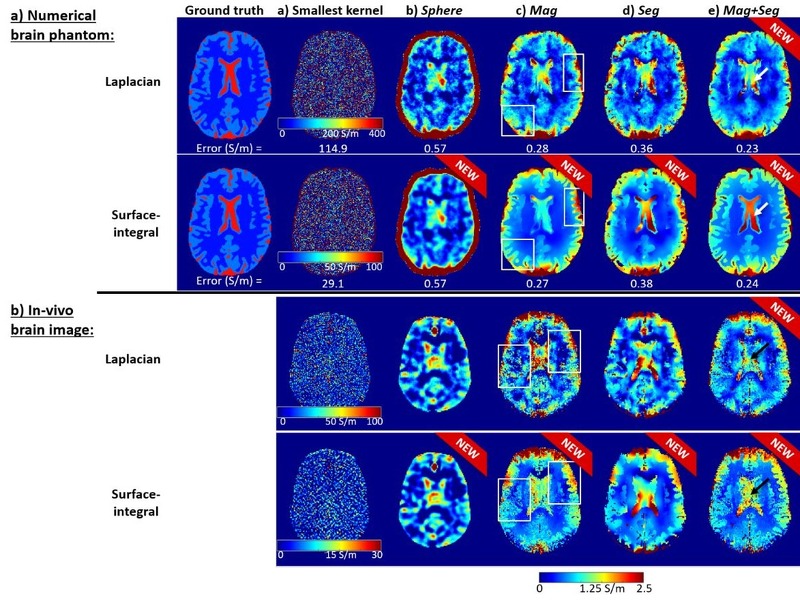
Figure 1: Optimised conductivity maps calculated using 10 different methods in an anthropomorphic brain phantom (top) and an in-vivo brain image (bottom). Mean absolute errors in the brain are also shown for the phantom. White rectangles highlight the superior performance of the integral-based methods.

1. Katscher, Ulrich, and Cornelius AT van den Berg. "Electric properties tomography: biochemical, physical and technical background, evaluation and clinical applications." NMR in Biomedicine 30.8 (2017): e3729.

2. Liao, Yupeng, et al. "Correlation of quantitative conductivity mapping and total tissue sodium concentration at 3T/4T." Magnetic resonance in medicine 82.4 (2019): 1518-1526.

3. Tha, Khin Khin, et al. "Noninvasive electrical conductivity measurement by MRI: a test of its validity and the electrical conductivity characteristics of glioma." European radiology 28.1 (2018): 348-355.

4. Karsa, Anita, and Shmueli, Karin. “Simultaneous Noise Suppression and Edge Preservation in Phase-based MRI Conductivity Mapping.” Proceedings of the Annual Meeting of the ESMRMB. (2020).

5. Lee, Joonsung, Jaewook Shin, and Dong‐Hyun Kim. "MR‐based conductivity imaging using multiple receiver coils." Magnetic resonance in medicine 76.2 (2016): 530-539.

6. Shin, Jaewook, et al. "Initial study on in vivo conductivity mapping of breast cancer using MRI." Journal of Magnetic Resonance Imaging 42.2 (2015): 371-378.

7. Katscher, Ulrich, et al. "Estimation of breast tumor conductivity using parabolic phase fitting." Adapting MR in a Changing World: ISMRM 20th Annual Meeting, Melbourne, Australia, 5-11 May 2012.

8. Voigt, Tobias, Ulrich Katscher, and Olaf Doessel. "Quantitative conductivity and permittivity imaging of the human brain using electric properties tomography." Magnetic Resonance in Medicine 66.2 (2011): 456-466.

9. Bulumulla, Selaka Bandara, Seung-Kyun Lee, and Teck Beng Desmond Yeo. "Calculation of electrical properties from B1+ maps-a comparison of methods." Brain 68.65.7 (2012): 66-2.